루나의 TIL 기술 블로그

프로그래머스 level 1 소수 만들기

05 Jul 2021 | 기초 프로그래머스 TIL

걸린 시간 : 2시간

문제 설명

주어진 숫자 중 3개의 수를 더했을 때 소수가 되는 경우의 개수를 구하려고 합니다. 숫자들이 들어있는 배열 nums가 매개변수로 주어질 때, nums에 있는 숫자들 중 서로 다른 3개를 골라 더했을 때 소수가 되는 경우의 개수를 return 하도록 solution 함수를 완성해주세요.

입출력 예

nums result
[1,2,3,4] 1
[1,2,7,6,4] 4

사고과정

세 개의 숫자를 조합으로 뽑아서 더한 뒤 소수인지 판별한다.

제출답안

from itertools import combinations
#조합(중복을 허용하지 않고 순서를 고려하지 않는다)
def isPrime(n): #소수인지 판별하는 함수
    for i in range(2,n): #2부터 n까지 돌면서
        if n % i == 0: #n이 나누어지면 
            return False #거짓
    return True #나누어지지 않으면 참 반환

def solution(nums):
    sum_nums = []
    prime_nums = []
    for i in combinations(nums, 3): #숫자 3개를 뽑는다
        sum_nums.append(sum(i)) 
        #세 숫자의 합을 sum_nums에 넣는다.
        #주의 : 같은 숫자여도 다른 조합이기 때문에 세어준다. (set 사용 X)

    for num in sum_nums:
        if isPrime(num): #소수라면
            prime_nums.append(num)
            #prime_nums에 넣는다
       
    return len(prime_nums)
    #prime_nums의 갯수를 반환한다

주요 포인트 및 생각해볼 점

소수를 판별하는 algorithm은 시간복잡도에 따라 이런 방법들이 있었다. 출처: 코요님의 벨로그

  1. 그냥 나누기 (O(X))
  2. 제곱근까지 살펴보기 (O(X^1/2))
  3. 에라토스테네스의 체 (O(NloglogN))

소수를 판별하는 algorithm을 쓰는 과정에서 전에 약수를 구할 때 썼던 제곱근까지 살펴보는 개념이 나와서 뿌듯했다. 에라토스테네스의 체는 어떤 수의 배수를 모두 제거해나가면서 소수를 찾는 과정이다.

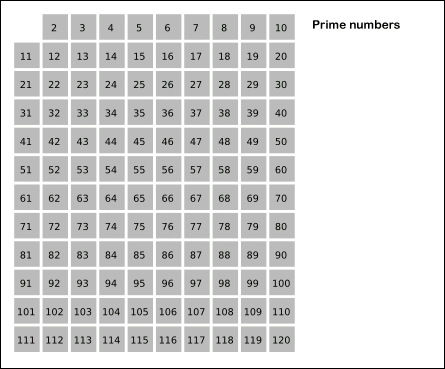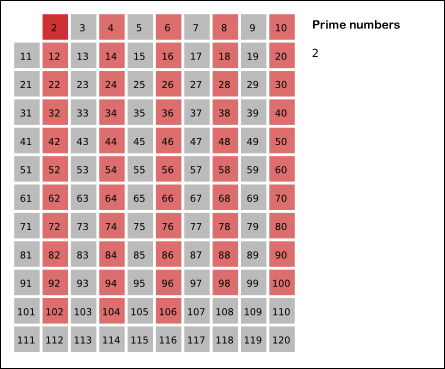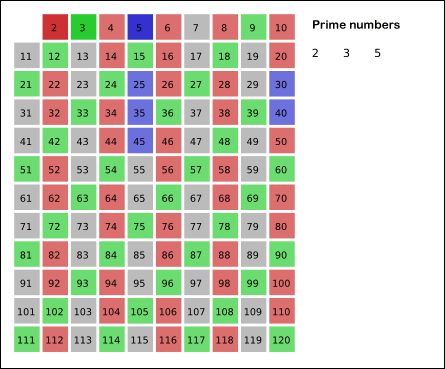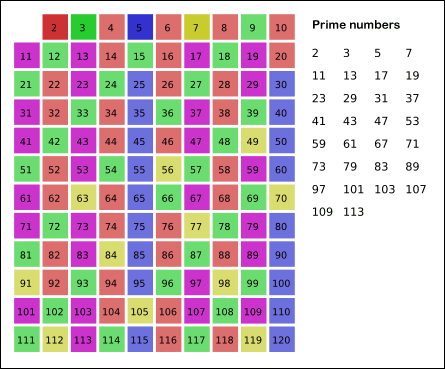
에라토스테네스의 체

소수만들기에서 사용했던 소수를 판별하는 함수(isPrime)와 소수리스트를 출력하는 함수(solution)를 한 개의 함수로 만들고 싶었는데 잘 안됐다.

오늘은 위코드 의 첫날이었는데 앞으로 함께 팀프로젝트를 진행하고 동기들과 친해질 생각에 기대가 된다.

Related Posts